474. 一和零

[力扣原题链接](https://leetcode-cn.com/problems/ones-and-zeroes/)

## 题目

给你一个二进制字符串数组`strs`和两个整数`m`和`n`。

请你找出并返回`strs`的最大子集的大小，该子集中 最多有`m`个`0`和`n`个`1`。

如果`x`的所有元素也是`y`的元素，集合`x`是集合`y`的子集 。

**示例 1:**

```
输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。
```

**示例 2:**

```
输入：strs = ["10", "0", "1"], m = 1, n = 1
输出：2
解释：最大的子集是 {"0", "1"} ，所以答案是 2 。
```

**提示：**

* `1 <= strs.length <= 600`
* `1 <= strs[i].length <= 100`
* `strs[i] 仅由 '0' 和 '1' 组成`
* `1 <= m, n <= 100`

## 思路
**官方题解：**
这道题和经典的背包问题非常相似，但是和经典的背包问题只有一种容量不同，这道题有两种容量，即选取的字符串子集中的`0`和`1`的数量上限。

经典的背包问题可以使用二维动态规划求解，两个维度分别是物品和容量。这道题有两种容量，因此需要使用三维动态规划求解，三个维度分别是字符串、`0`的容量和`1`的容量。

定义三维数组`dp`，其中`dp[i][j][k]`表示在前`i`个字符串中，使用`j`个`0`和`k`个`1`的情况下最多可以得到的字符串数量。假设数组`str`的长度为`l`，则最终答案为 `dp[l][m][n]`。

当没有任何字符串可以使用时，可以得到的字符串数量只能是`0`，因此动态规划的边界条件是：当`i=0`时，对任意`0≤j≤m`和`0≤k≤n`，都有`dp[i][j][k]=0`。

当`1≤i≤l`时，对于`strs`中的第`i`个字符串（计数从`1`开始），首先遍历该字符串得到其中的`0`和`1`的数量，分别记为`zeros`和`ones`，然后对于`0≤j≤m` 和`0≤k≤n`，计算`dp[i][j][k]`的值。

当`0`和`1`的容量分别是`j`和`k`时，考虑以下两种情况：

如果`j<zeros`或`k<ones`，则不能选第`i`个字符串，此时有`dp[i][j][k]=dp[i−1][j][k]`；

如果`j≥zeros`且`k≥ones`，则如果不选第`i`个字符串，有`dp[i][j][k]=dp[i−1][j][k]`，如果选第`i`个字符串，有`dp[i][j][k]=dp[i−1][j−zeros][k−ones]+1`,`dp[i][j][k]`的值应取上面两项中的最大值。

因此状态转移方程如下：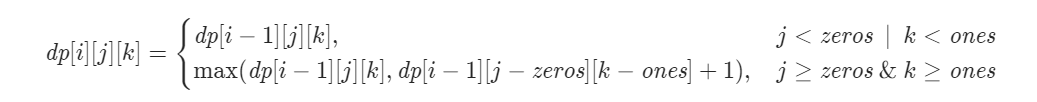

![](/media/202106/2021-06-06_190352.png)

最终得到`dp[l][m][n]`的值即为答案。
由此可以得到空间复杂度为`O(lmn)`的实现。

由于`dp[i][][]`的每个元素值的计算只和 `dp[i−1][][]`的元素值有关，因此可以使用滚动数组的方式，去掉`dp`的第一个维度，将空间复杂度优化到 `O(mn)`。

实现时，内层循环需采用倒序遍历的方式，这种方式保证转移来的是`dp[i−1][][]`中的元素值。

## 代码

语言：Java

```
class Solution {
    /**
     * 动态规划（背包问题）
     *
     * @param strs
     * @param m
     * @param n
     * @return
     */
    public int findMaxForm(String[] strs, int m, int n) {
        int[][] dp = new int[m+1][n+1];
        int length = strs.length;
        for (int i = 0; i < length; i++) {
            List<Integer> list = countNum(strs[i]);
            int zeroNum = list.get(0);
            int oneNum = list.get(1);
            for (int j = m; j >= zeroNum; j--) {
                for (int k = n; k >= oneNum; k--) {
                    dp[j][k] = Math.max(dp[j][k], dp[j-zeroNum][k-oneNum]+1);
                }
            }
        }

return dp[m][n];
    }

/**
     * 计算每个字符串中1和0的数量
     * 
     * @param str
     * @return
     */
    public List<Integer> countNum(String str) {
        char[] nums = str.toCharArray();
        int zeroCount = 0;
        int oneCount = 0;
        for (int i = 0; i < nums.length; i++) {
            if(nums[i] == '0') {
                zeroCount++;
            } else {
                oneCount++;
            }
        }
        List<Integer> list = new ArrayList<>();
        list.add(zeroCount);
        list.add(oneCount);
        return list;
    }
}
```